[新しいコレクション] 平行 四辺 形 面積 問題 326130

 平行四辺形の面積の問題です。 公式は難しいものではありませんが、底辺と高さをしっかり理解するようにしてください。 ポイント 平行四辺形の1つの辺を底辺とするとき、底辺に向かい合う辺まで垂直にひいた直線の長さを高さといいま 平行線と面積に関する問題です。ポイント平行線と面積に関する問題は以下のことをしっかり確認しておきましょう。平行線にはさまれた三角形の面積は等しい面積が等しい三角形の頂点を通る直線は平行例）下の図で abcと dbc面積が等しい → abc= dbc とかく。公園に芝生（しばふ）を植えよう （平行四辺形や三角形の面積） どちらが広いでしょうか（平行四辺形や三角形の面積） どちらが多く食べたかな？（三角形の面積） 折り紙でかざりを作ろう①（平行四辺形や三角形の面積） 折り紙でかざりを作ろう②

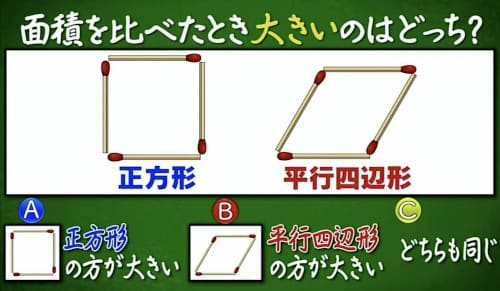
正方形と平行四辺形の面積の話 クイズ あなたは小学５年生より賢いの 12 25 何ゴト

平行 四辺 形 面積 問題

平行 四辺 形 面積 問題-ひし形の面積は 2 2 つの対角線の長さをかけて2で割ったもの、つまり 『対角線×対角線÷2 ÷ 2 』 で求めることができます。 平行四辺形の一種でもあるので、底辺と高さが分かっていれば『底辺×高さ』でも求められます。 たとえば以下のような問題の場合 四角形ebfd＝96－36－36＝24 24cm 別解 平行四辺形の面積の割合を1とする。 abeの割合が全体の bcfの割合が全体のの であるから、四角形ebfdの割合は よって四角形ebfdの面積は cm ＊)平行四辺形の面積の割合を1とせず面積をsとしてもよい。

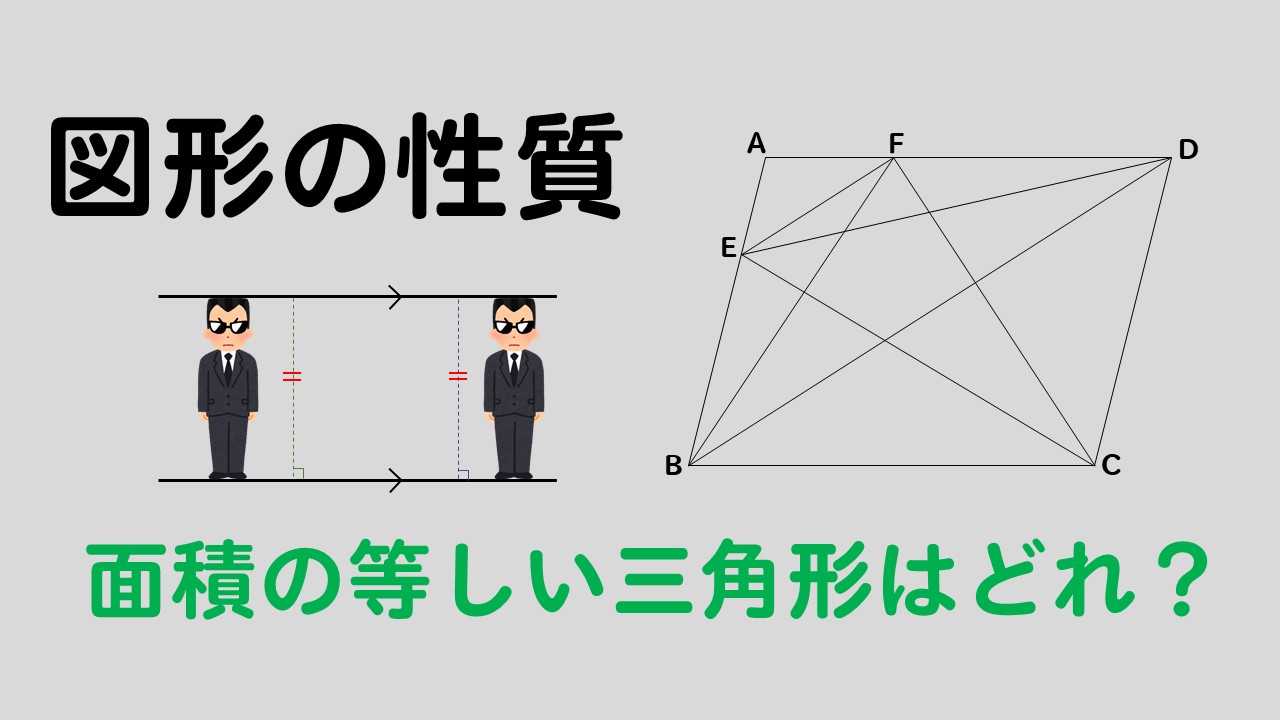
中2数学 平行四辺形の中から面積の等しい三角形を見つける問題を解説 数スタ

平行四辺形を二等分するような直線の式を考えなさい。 というような問題がよく出題されます。 この問題を解くためには、ちょっとした特徴を知っておく必要があります。 それが 対角線が交わる点を通るように 直線をひくと、平行四辺形を二等分できる！ 目次 平行線と三角形の面積 等積変形の作図 ①四角形から三角形を作る ②折れ線を直線にする ③五角形から三角形を作る 等積変形の利用① (平行四辺形の中の三角形) 等積変形の利用② (面積を求める) 平行線と面積 (等積変形)のまとめ 平行四辺形と長方形の面積は同じになるので、平行四辺形の道の面積も右端に寄せてしまいます。 中の長方形の面積を求めます。 ×30＝600㎡ 例3）頂点をまとめて考えます。 ＊平行四辺形の中の色のついた部分の面積を求めます。 頂点をまとめると下の図

以上で二つのベクトルが作る平行四辺形の面積は、それらのベクトル積の大きさに等しいことがわかりました。 ベクトル \(\overrightarrow{a} = \langle2, 0, 0 \rangle\) と \(\overrightarrow{b} = \langle 1, 1, 0 \rangle\) が作る平行四辺形の面積を求めよ。平行四辺形の面積は，任意の直線で切断して長方形に等積変形すればよいことがわかり，求積す ることができる。 1問題場面をとらえる。 右の平行四辺形の面 積を求めましょう。 2面積の求め方を見通す。 「このままでは求められない。5年 平行四辺形の面積｜算数イメージ動画集｜大日本図書 平行四辺形の面積を求めるにはどうしたらいいでしょうか。 台形を2つ合わせて，あるいは三角形と台形を合わせて長方形にしてみると公式が使えます。 つまり，平行四辺形の面積は 底辺×高さ で

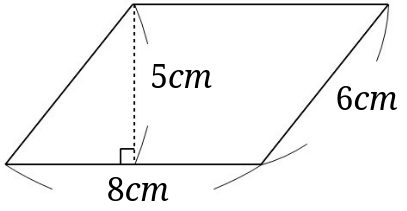
三角形 面積問題 平行四辺形 面積 図形問題 小学5年生 平行四辺形の面積もんだいは、底辺と高さを求めそれぞれを掛けるだけです すなわち 公式 底辺×高さ です 考え方は、面積のプリント①で説明してい なんとすれば、 （1）平行四辺形の二つの対角線は中点で交わるから、 一辺が等しい。 （2）対頂角は等しい （3）錯角が等しい よって、（1）～（3）より、一辺とその両端の角がそれぞれ 等しいので合同である。 したがって、黄緑色の三角形の面積は 平行四辺形の面積は、 「面積 底辺 高さ」 「 面 積 = 底 辺 × 高 さ 」 で求められます。 たとえば、「底辺 4 c m ,高さ 3 c m の平行四辺形」の面積は 4 × 3 = 12 c m 2 となります。 これは、平行四辺形の右端の直角三角形を切り取って左側に移すと 「たて 3 c m

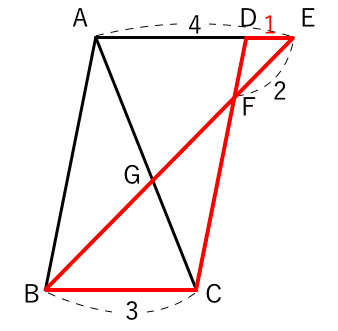
相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に

平面図形をマスター 三角形の面積比 応用編その２

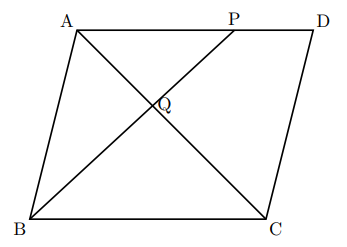
平行四辺形に対角線を引くと、2つの対角線が交わる点が、それぞれの対角線の中央にきます。 上記は平行四辺形の性質なので、是非理解しましょう。 平行四辺形の面積 平行四辺形の面積は、 底辺×高さ 問題 次の平行四辺形の面積を求めよ。 問題の解答・解説 これまでの説明を読んできた人は少し戸惑うかもしれません。 なぜなら、平行四辺形の高さに当たる値が問題の図では見当たらないからです。 これでは面積は求められそうもありません。ご覧いただきありがとうございます。以下、目次です127 三角形の面積の求め方 復習350 三角形の面積の求め方 参考522 問題の解き方(直線jkは辺ab

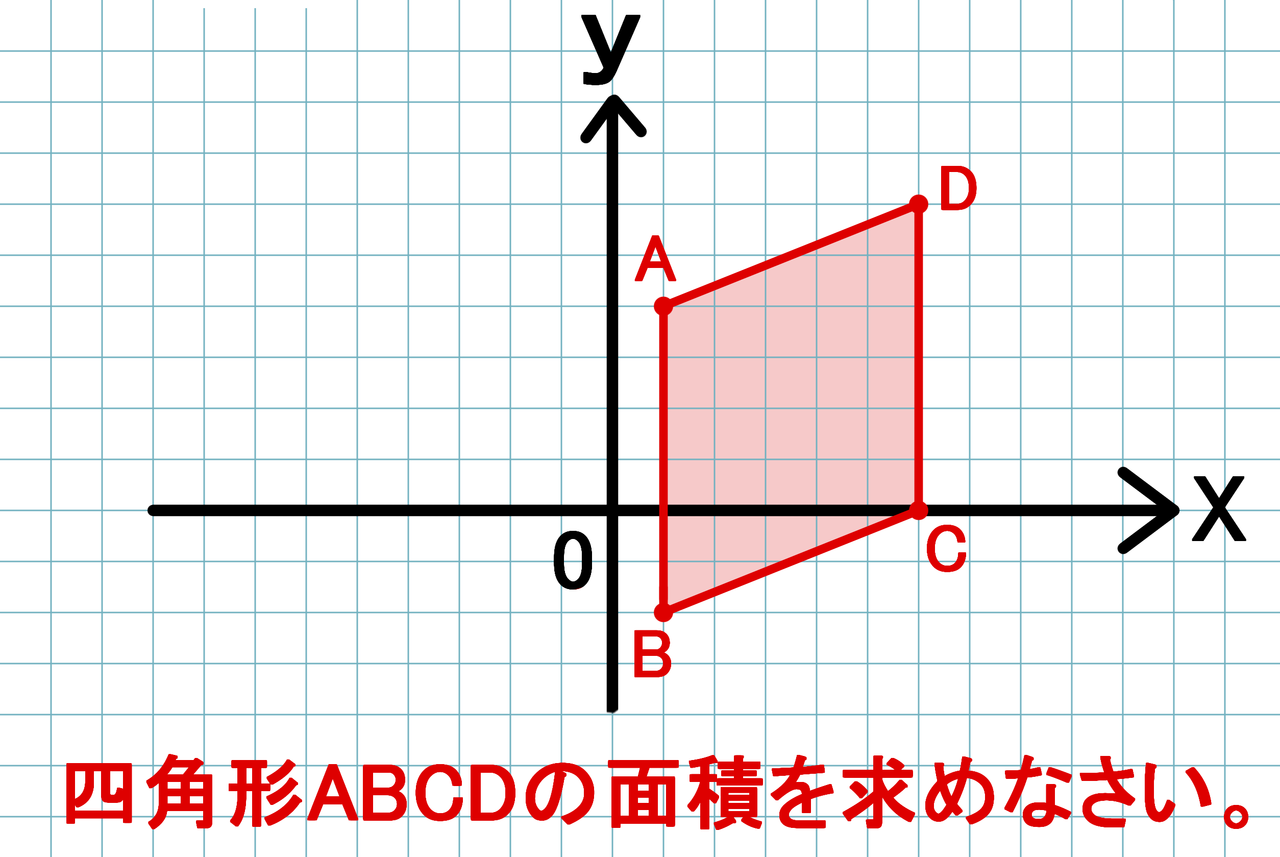
座標平面に描かれた図形に関する問題 バカでもわかる 中学数学

小学5年生の算数 動画 平行四辺形の面積の問題 底辺 高さ 19ch

平行四辺形の中から面積の等しい三角形を見つけれるようになりましたか？ 正直、慣れるまではなかなか難しい問題です。 平行四辺形に線がたくさんあって どこを見ていけばいいのか分かりにくいもんね。 だけど、何度も練習していると 問題 上図のように正三角形10個で作られた平行四辺形があります。 この平行四辺形の面積は300㎠です。 ここで問題です。 青色部分の面積を求めてください。 見た目は面白そうですが使う知識は数学の相似やら面積比やら、ごりごりに数学です。 相似平行四辺形 面積 図形問題 小学5年生平行四辺形の面積もんだいは、底辺と高さを求めそれぞれを掛けるだけですすなわち 公式 底辺×高さ です考え方は、面積のプリント①で説明しています平行四辺形 面積問題①平行四辺形 面積問題②平行四辺形面積の

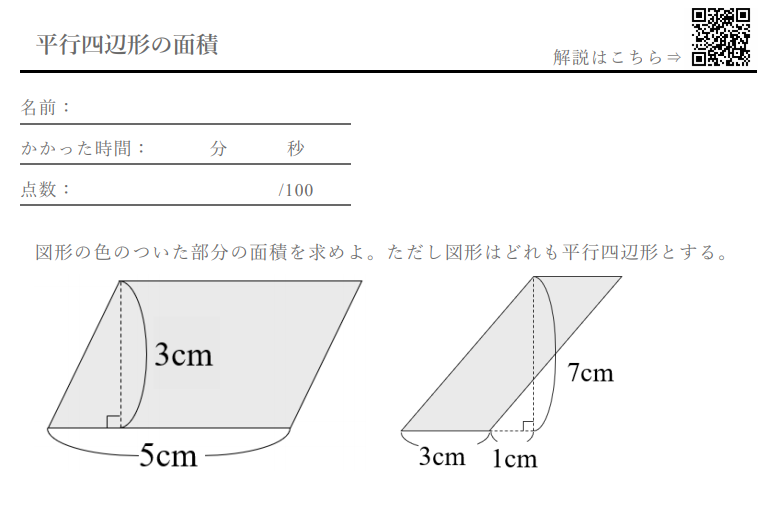
平行四辺形 の面積 計算ドリル 問題集 数学fun

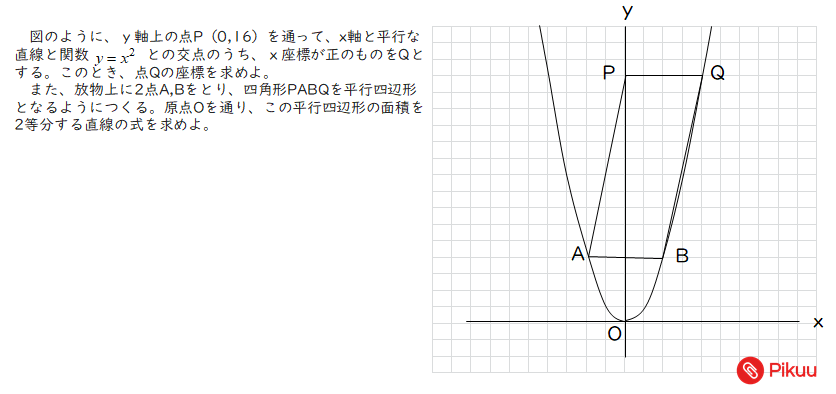
中学数学 平行四辺形の面積を二等分する直線を求める定期テスト予想問題 Pikuu

 図のように、平行四辺形の各辺の3等分点の一つと頂点を結んだ線を 引きます。網目部分の面積は平行四辺形の面積の何倍ですか。 答えは： 2／5倍 まず、僕の回答は面積の問題を解く上で、 平行四辺形を高さを変えず、長方形にしても 面積は変わらない平行四辺形 《 例 》 図のような abcd (= 平行四辺形abcd)のとき、br：rq を求めましょう → 「山ちょう」がありませんね → 「山ちょう」をつくる「補助線」ですね 補助線は色々引いてみてくださいね そうすれば「これかな！ 今回は、平行四辺形の面積の求め方について書いていきたいと思います。 平行四辺形の面積を求める公式 平行四辺形の面積を求める問題 問題① 《平行四辺形の面積の求め方》 問題② 《平行四辺形の面積の求め方》 問題③ 《平行四辺形の高さの求め方》 問題④ 《平行四辺形の底辺の求め方

関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ

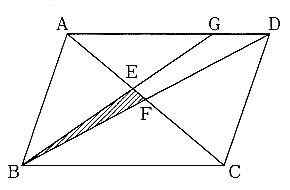
北辰塾 情報局 直撃 中学入試問題 第53回 鴎友学園女子中 面積比の問題

 小5の問題です。 斜線部の面積を求めます。答えは147平方センチメートル。 平行四辺形縦14㎝横21㎝の面積は 14×21＝294 294㎠ どこに点を打っても対する二つの三角形の面積を合わせると平行四辺形の半分になるようです。 こんにちは。平行四辺形と面積②です。それではどうぞ。 面積比の問題で, 1つの攻略方法として, 相似比の2乗から攻める方法を紹介しておりますが, 相似な関係がない場合は, 役に立ちません。そこで, 相似な関係がなくてもで な問題が，21の都立西にあったのでご紹介します。 問1，問2中2の図形証明分野習った後に解ける 問3相似習った後に解ける 芸術的な難問高校入試 第52回 「平行四辺形の超難しい証明」 出典：令和3年度 都立西高校（独自作成校） 過去問 数学 範囲

3

子どもを混乱させる相似な三角形の２つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生

小学4年生の算数 台形・平行四辺形・ひし形・対角線 問題プリント 小学4年生の算数・台形・平行四辺形・ひし形・対角線の問題を繰り返し練習できるプリントです。各単元の「問題一括」または「解答一括」をクリックすると、新しいウィンドウ（またはタブ）にPDFファイル が表示されます。 保存または直接印刷してください。 軸と直線で囲まれた三角形の面積 特別な平行四辺形相似比の練習問題（平行四辺形1） 問1．次の各問いに答えなさい。 (ｱ) abcd においてae：ed ＝2：1 で efd の面積が2 cm 2のとき (1) cfd の面積 (2) bcf の面積 (3) abcd の面積 (ｲ)右の平行四辺形abcd で、辺ab の中点をe、対角線bd とce の交点をf とするとき

すきるまドリル 小学５年生 算数 図形の面積 無料学習プリント すきるまドリル 無料学習プリント

5年生算数ドリル 面積

平方四辺形の面積 小５の問題です 斜線部の面積を求めます 答えは14 小学校 教えて Goo

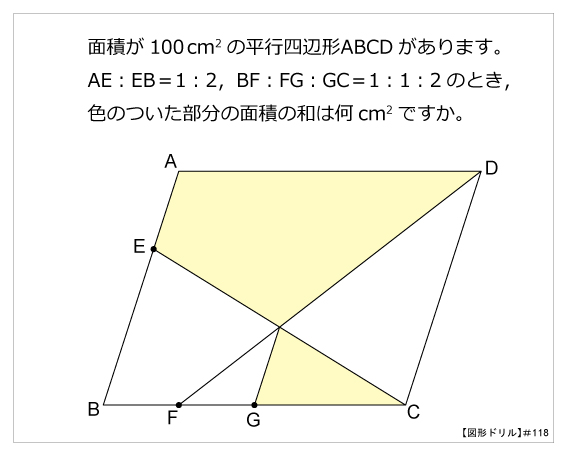
第118問 平行四辺形の面積の和 図形ドリル 第118問 平行四辺形の面積の和 算数星人のweb問題集 中学受験算数の問題に挑戦

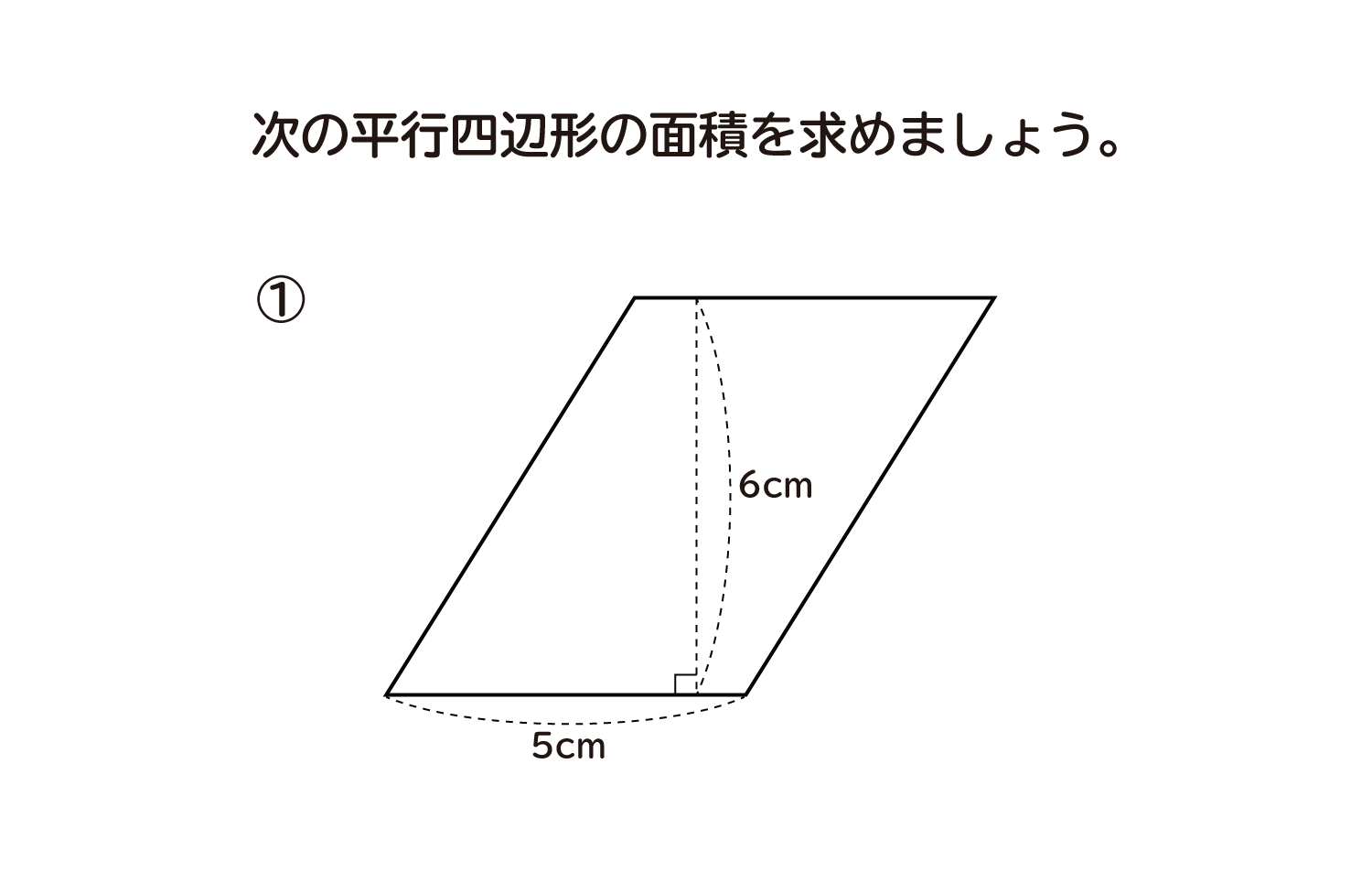
小学5年生 算数 無料問題集 平行四辺形の面積 おかわりドリル

高校数学 平行四辺形の面積の求め方 例題編 映像授業のtry It トライイット

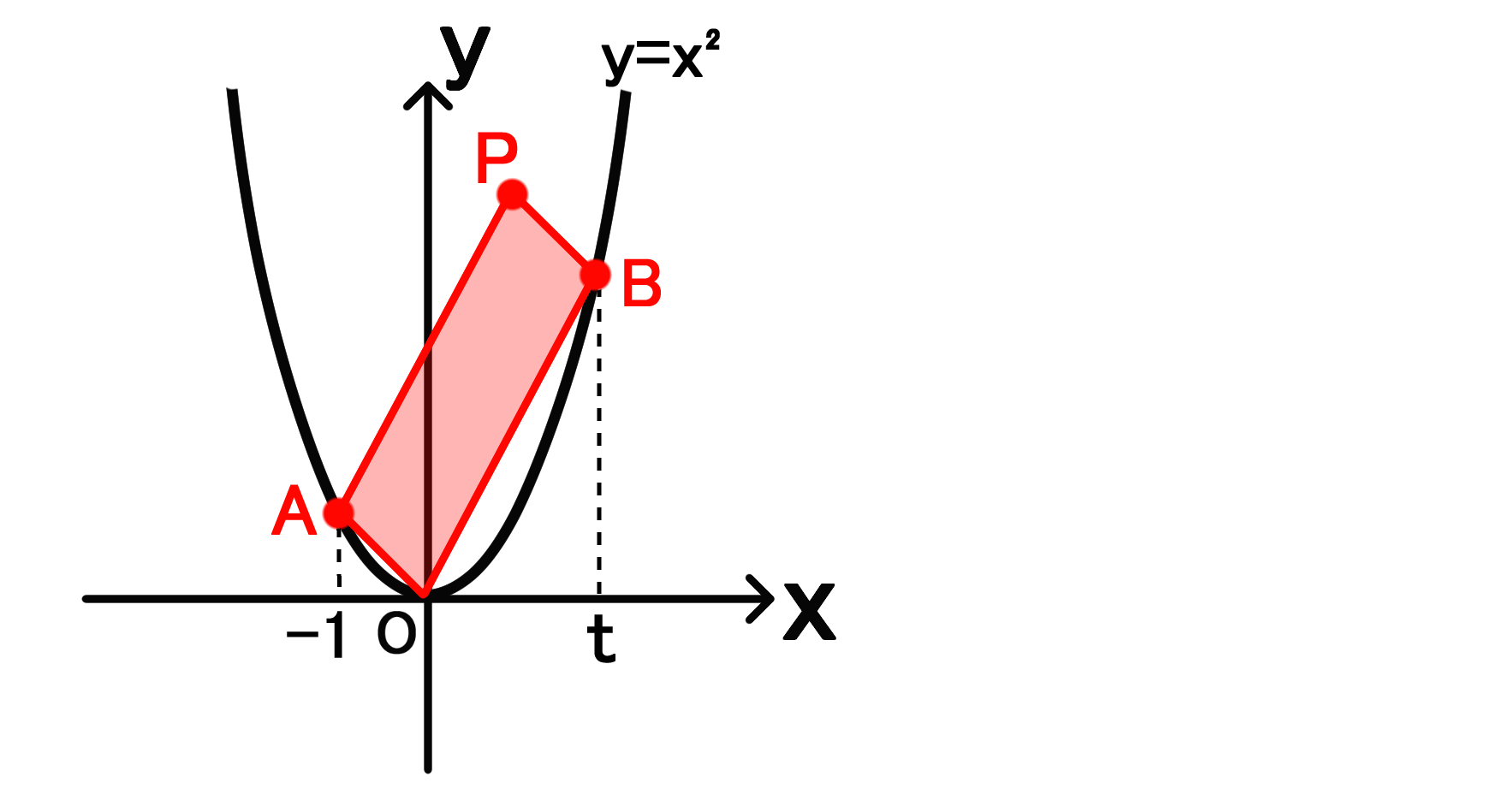
放物線y X 上の点を結ぶと平行四辺形になる問題 バカでもわかる 中学数学

平行四辺形の面積の求め方 公式と計算例

小５ 算数 小５ ４１ 平行四辺形の面積 Youtube

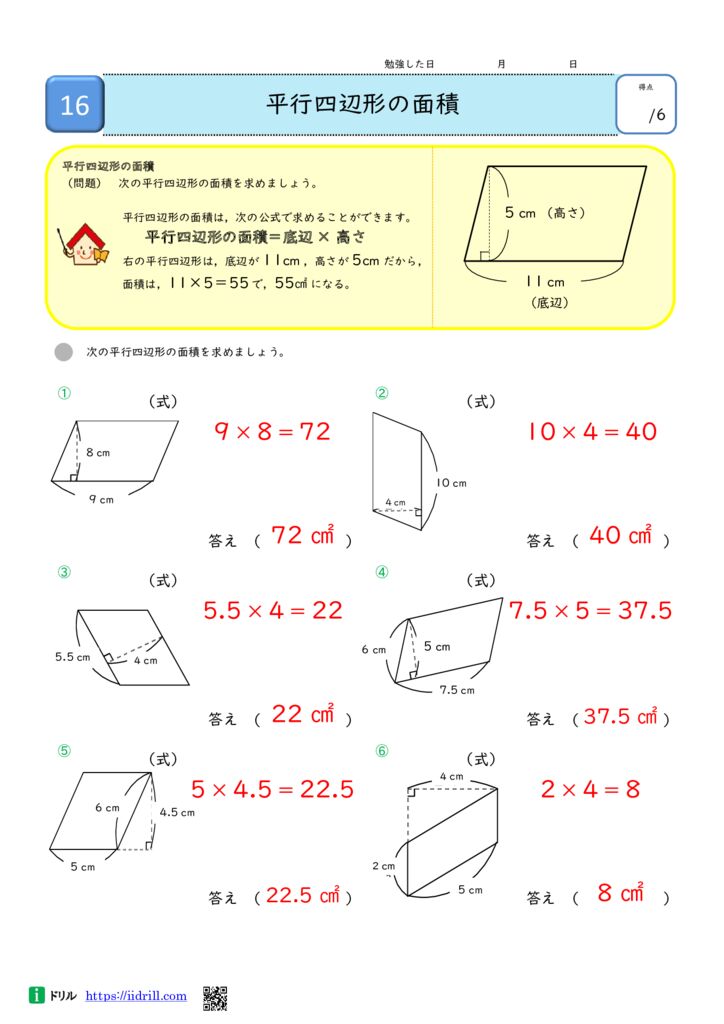
5年生算数ドリル 面積

数学検定準2級 2次 過去問 お願いします Clearnote

中学 数学 平行四辺形の面積の問題です 中学 数学 平行四辺形の 数学 教えて Goo

平行四辺形で知っておくべきこと 苦手な数学を簡単に

小学5年生 算数 無料問題集 平行四辺形の面積 おかわりドリル

5年 平行四辺形の面積 算数イメージ動画集 大日本図書

ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun

今年の入試問題にチャレンジ 図形篇 後篇

面積問題 小学４から6年生 算数問題プリント

色のついた部分の面積の求め方 小学生

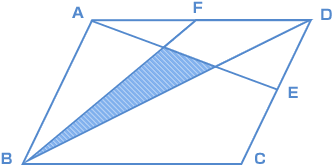
算数 平面図形と比 1 中学受験 ベネッセ教育情報サイト

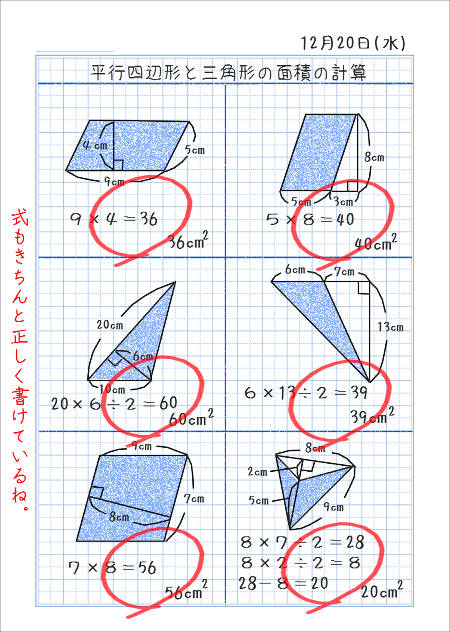
平行四辺形と三角形の面積 家庭学習レシピ

面積 上 面積の意味から 正方形 長方形 平行四辺形 三角形の面積の求め

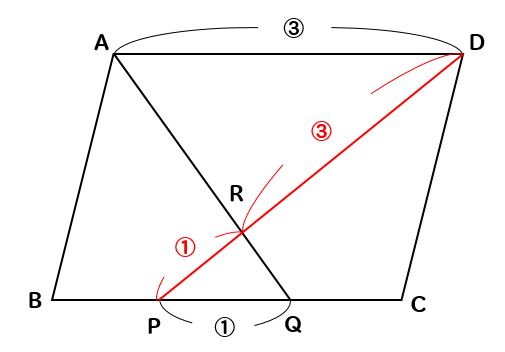
相似 平行四辺形と面積比の問題を徹底解説 数スタ

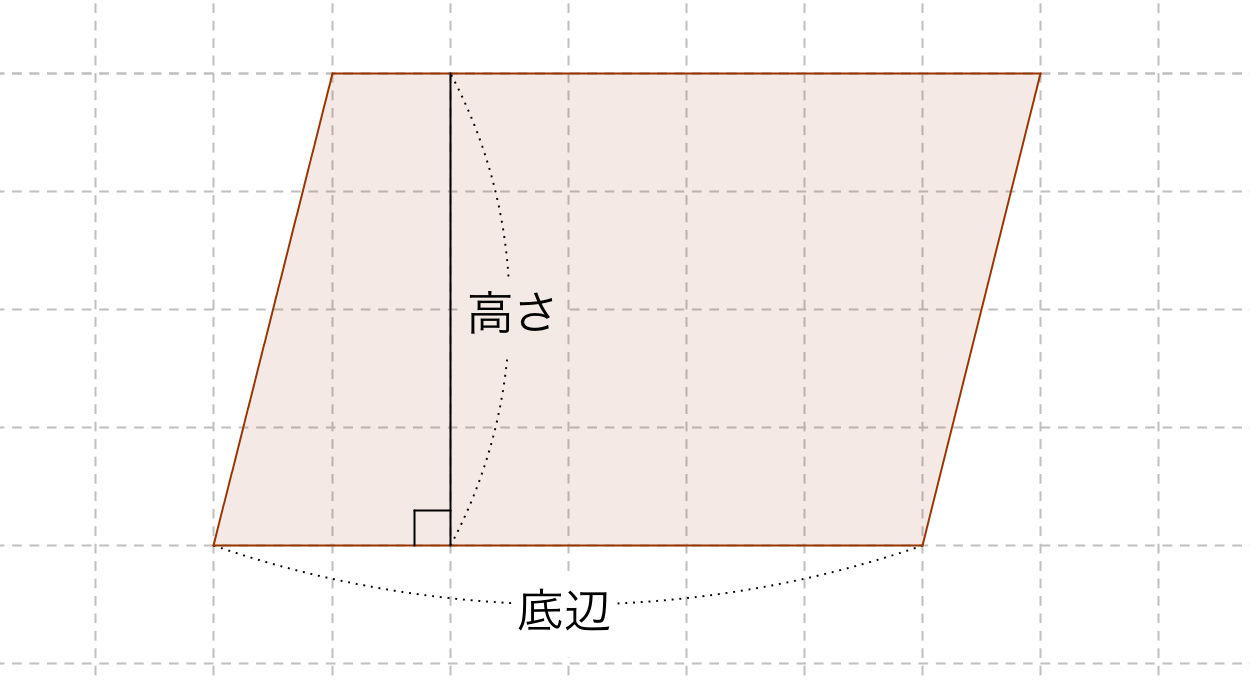
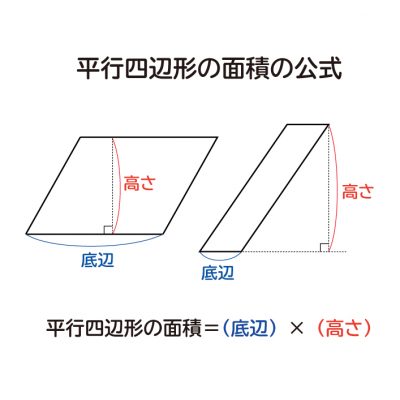
平行四辺形の面積の公式 算数の公式

中2数学 平行四辺形の中から面積の等しい三角形を見つける問題を解説 数スタ

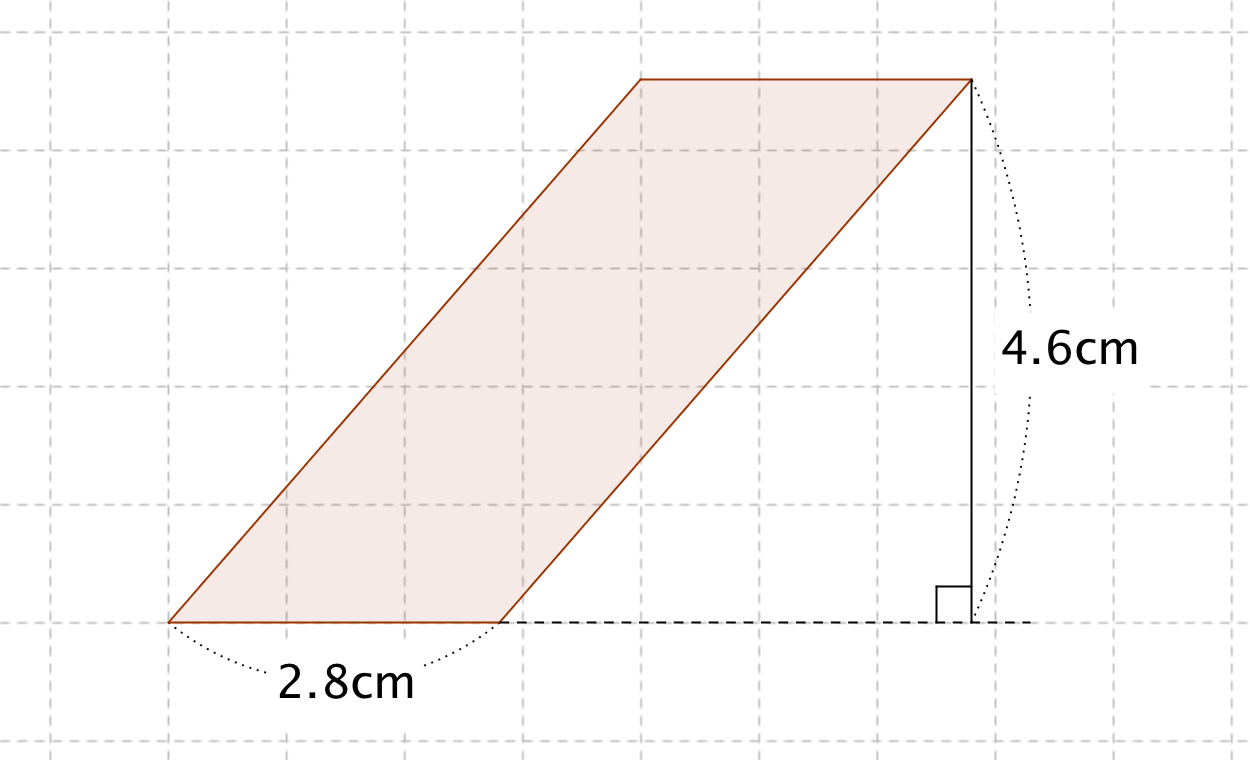
平行四辺形の面積の公式 算数の公式

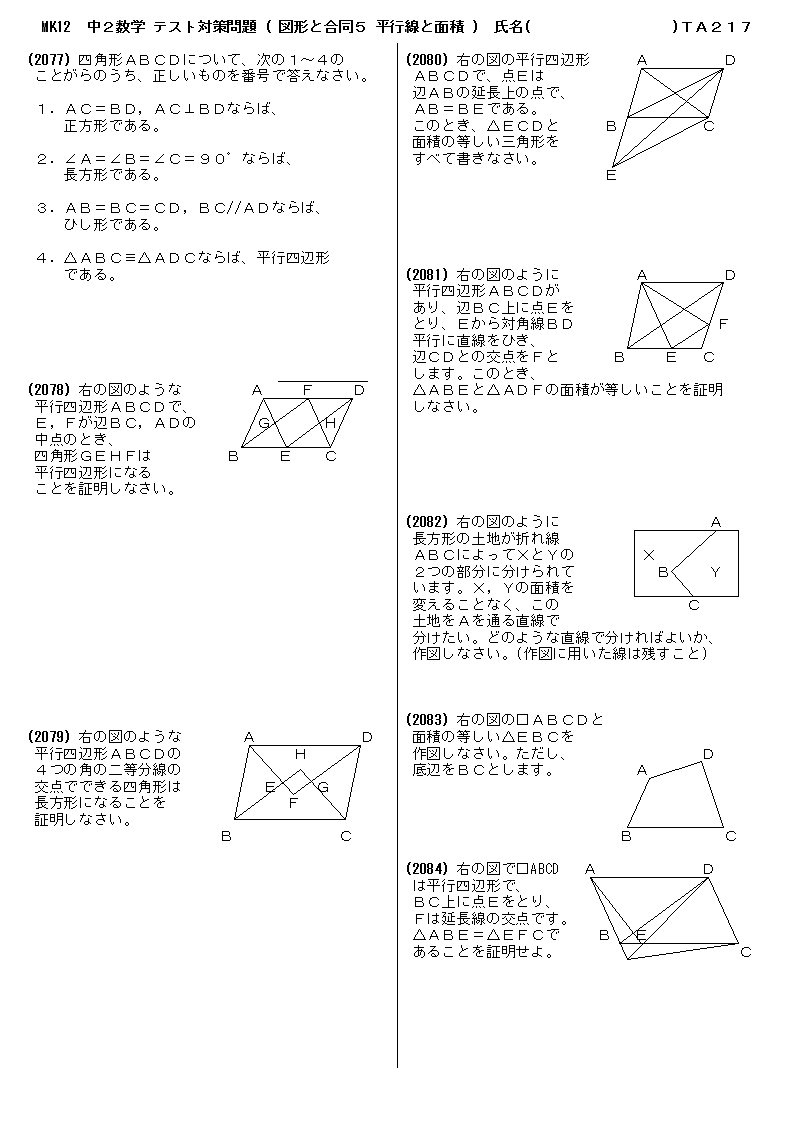
無料 中２数学 テスト対策 問題プリント 217 図形と合同５ 平行線と面積

簡単公式 平行四辺形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中点連結定理とは 逆の証明や平行四辺形の問題もわかりやすく解説 遊ぶ数学

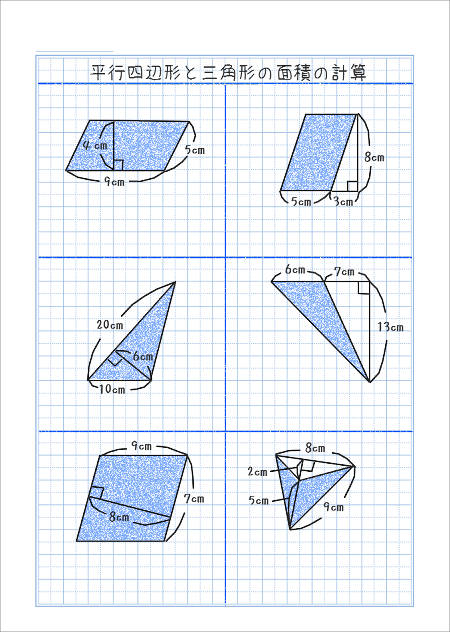
平行四辺形と三角形の面積 家庭学習レシピ

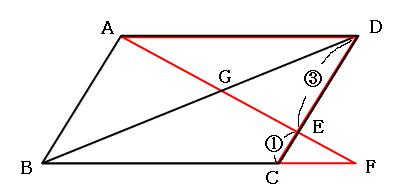
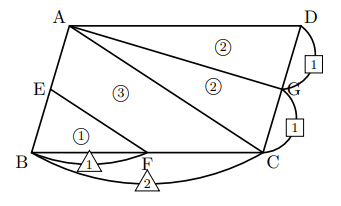
平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ

平行四辺形abcdの面積が24 であるとき 影をつけた部分の面積 Yahoo 知恵袋

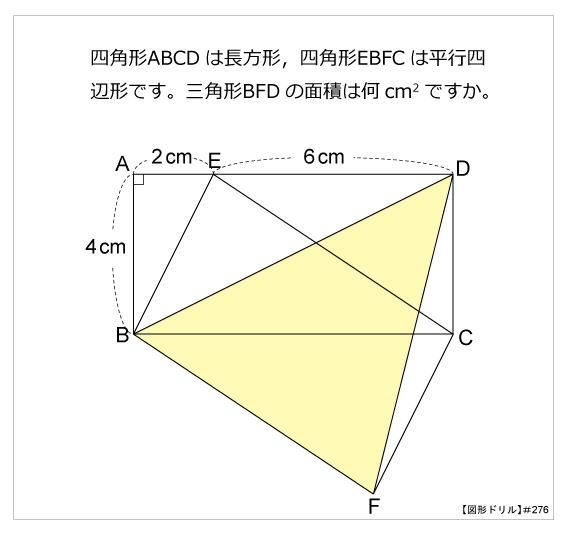
第276問 長方形と平行四辺形 図形ドリル 第276問 長方形と平行四辺形 算数星人のweb問題集 中学受験算数の問題に挑戦

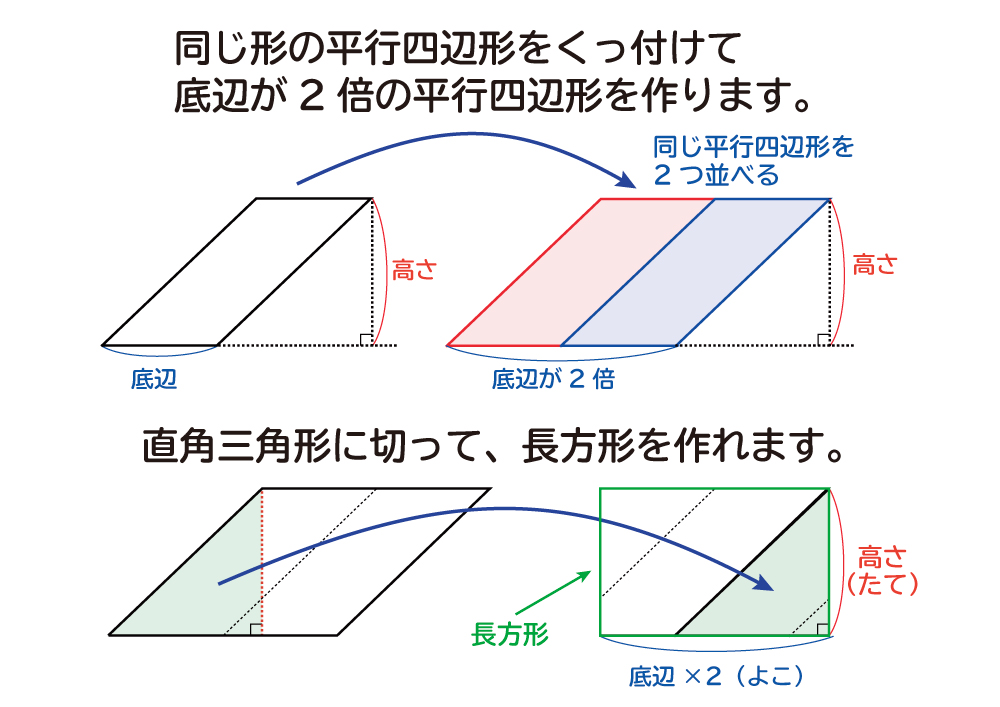
なぜ 平行四辺形の面積は 底辺 高さ なのか を説明します おかわりドリル

平行四辺形の部分面積は パズル算数クイズ

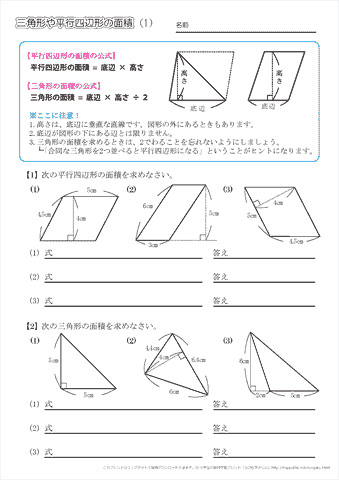
小学５年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生

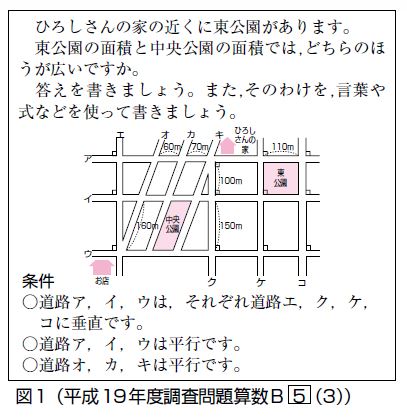
ブンブンぱぁとなぁweb 子供の考える力 書く力はこうすれば伸びる

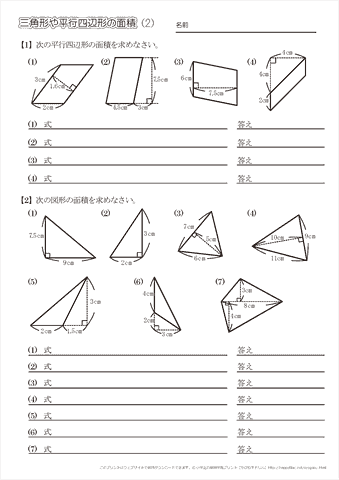
小学５年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生

公式なんて覚えない ひし形の面積は直感的に考えよう

3 の平行四辺形の面積の求め方を教えてください 答えです 42 Clearnote

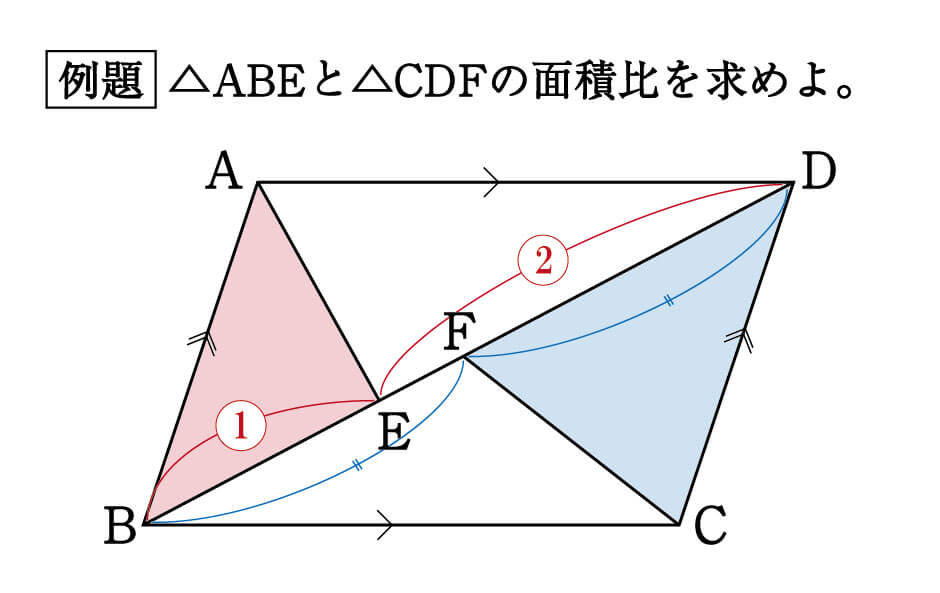
平行四辺形の面積比

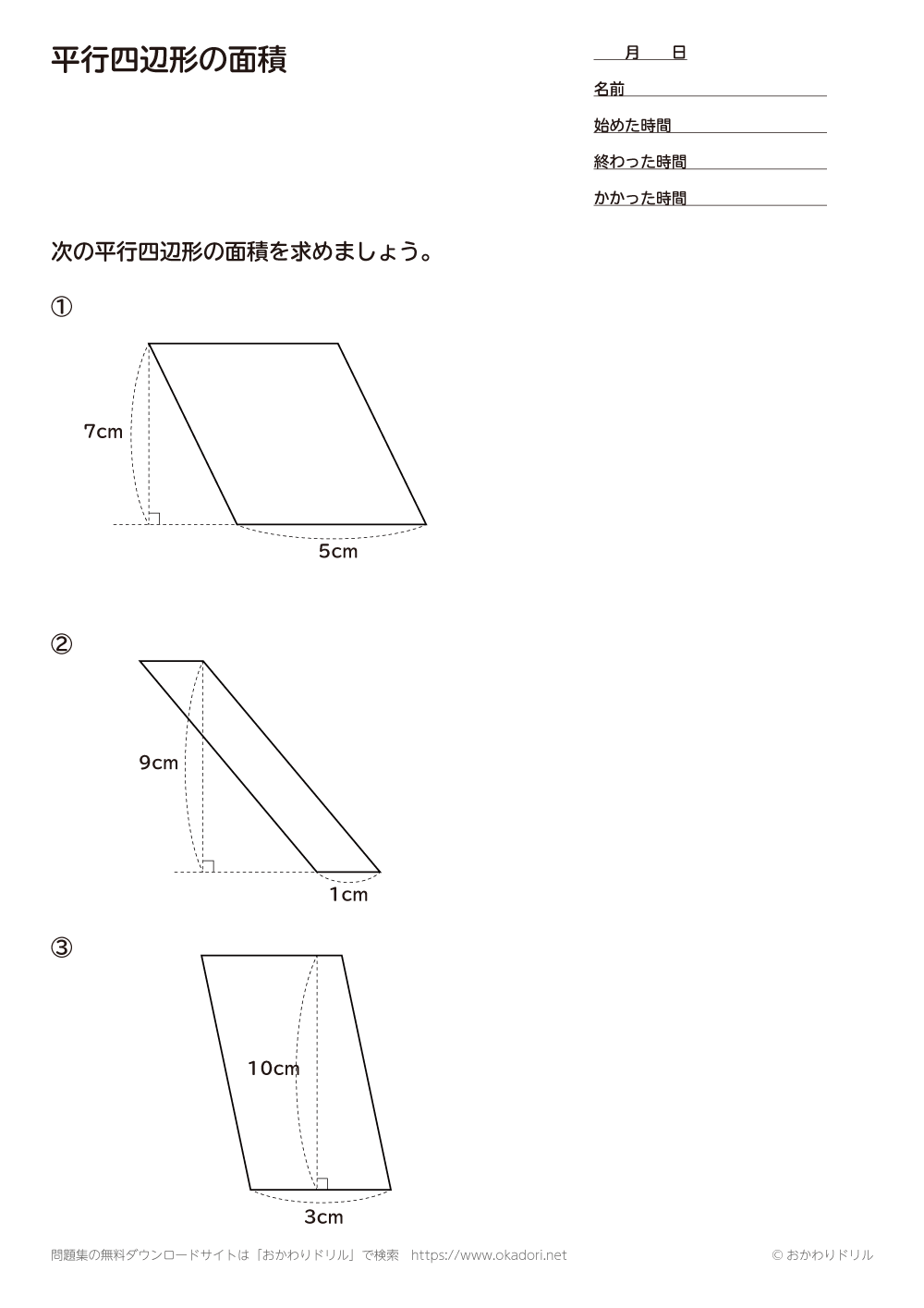
小学5年生 算数 無料問題集 平行四辺形の面積 おかわりドリル

Tikz 年度 群馬県前期の問題 平行四辺形と面積 数樂管理人のブログ

平行四辺形の面積 ベクトルでの公式 理数系無料オンライン学習 Kori

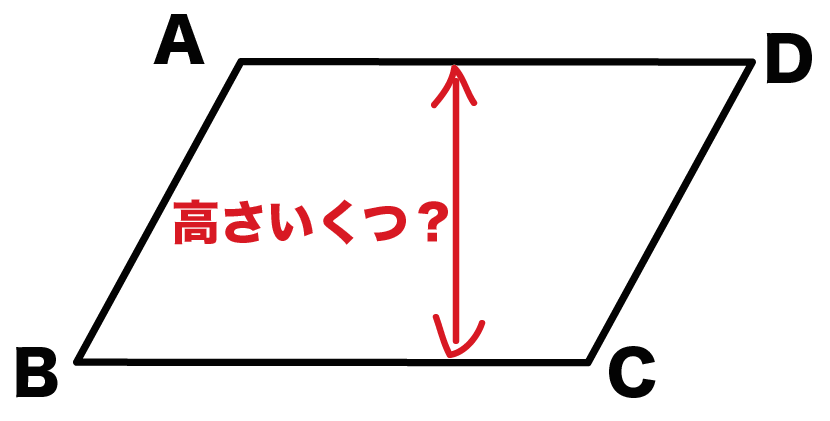
中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく

平行四辺形 算数解法の極意

パパしゅく 算数 ５年生 平行四辺形の面積 平行四辺形の色のついた面積を求める問題を作成しました 詳しくはパパしゅくをご覧ください Sites Google Com Site Shogakutezukurimondaishu Home 5nensei Muke Tedzukuri Mondai Shuu

攻略法 平行四辺形と面積 数樂管理人のブログ

平行四辺形のなかの三角形の相似や角度 長さ 等しい面積の求め方 現役塾講師のわかりやすい中学数学の解き方

平行四辺形の面積比の問題 解き方を教えてください Yahoo 知恵袋

無料 中２数学 発展問題 解答プリント 233 平行四辺形４

平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典

子どもを混乱させる相似な三角形の２つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生

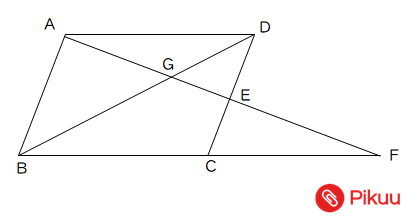
高校入試対策数学 面積比に関する対策問題 Pikuu

四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ

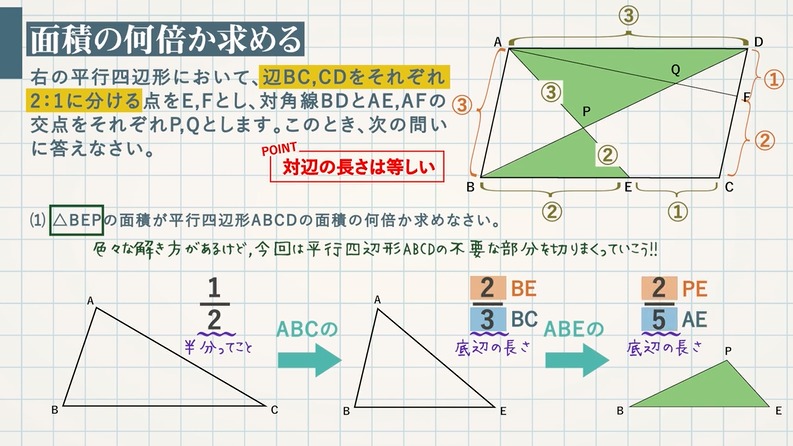
相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者

数学 なぜ面積比は苦手になりがちなの 面積比 集中特訓 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

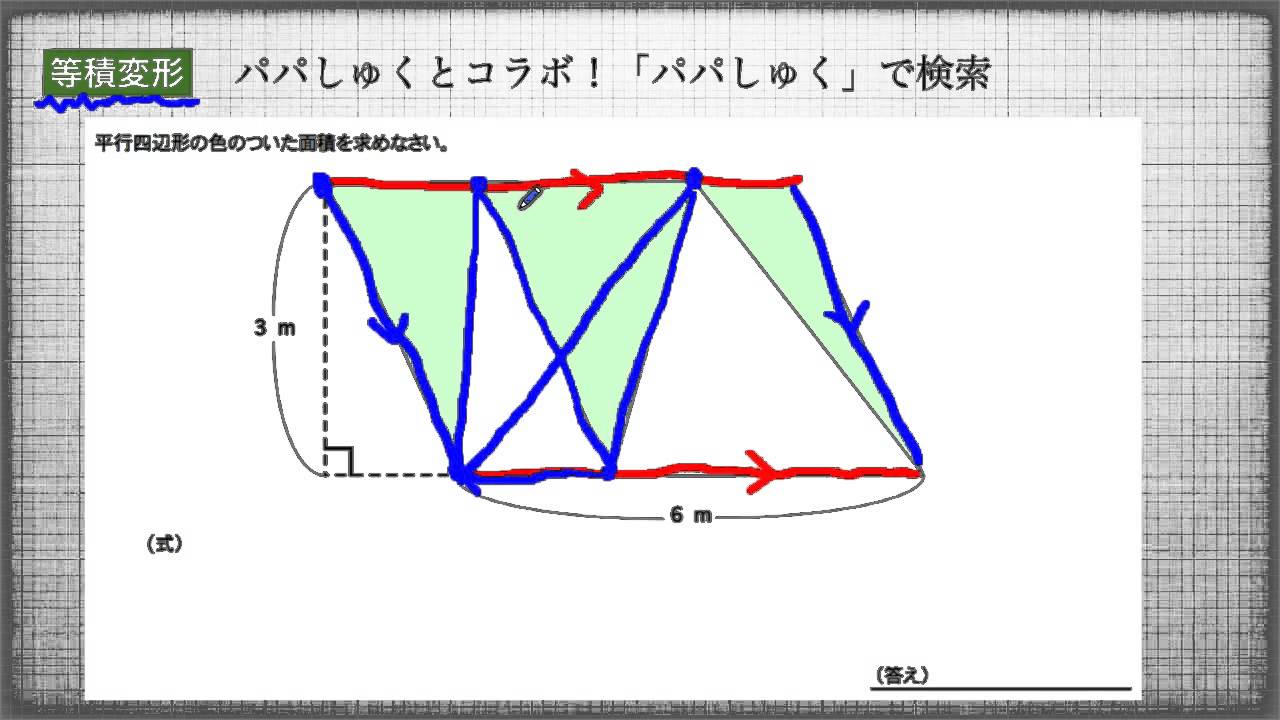
小学校５年 算数 面積 等積変形 問題編 パパしゅくとコラボしたよ Youtube

平行四辺形の面積の求め方で習う公式は なぜ底辺 高さになるの みけねこ小学校

攻略法 平行四辺形と面積 数樂管理人のブログ

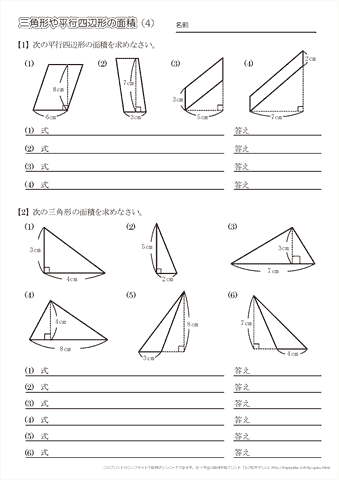
小学５年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生

今月の問題 平行四辺形

平面図形と比 平行四辺形の面積比 Next Stageのブログ

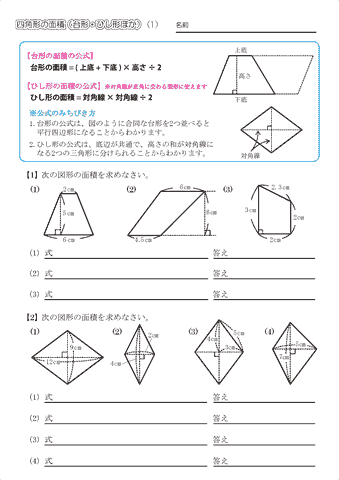
小学５年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生

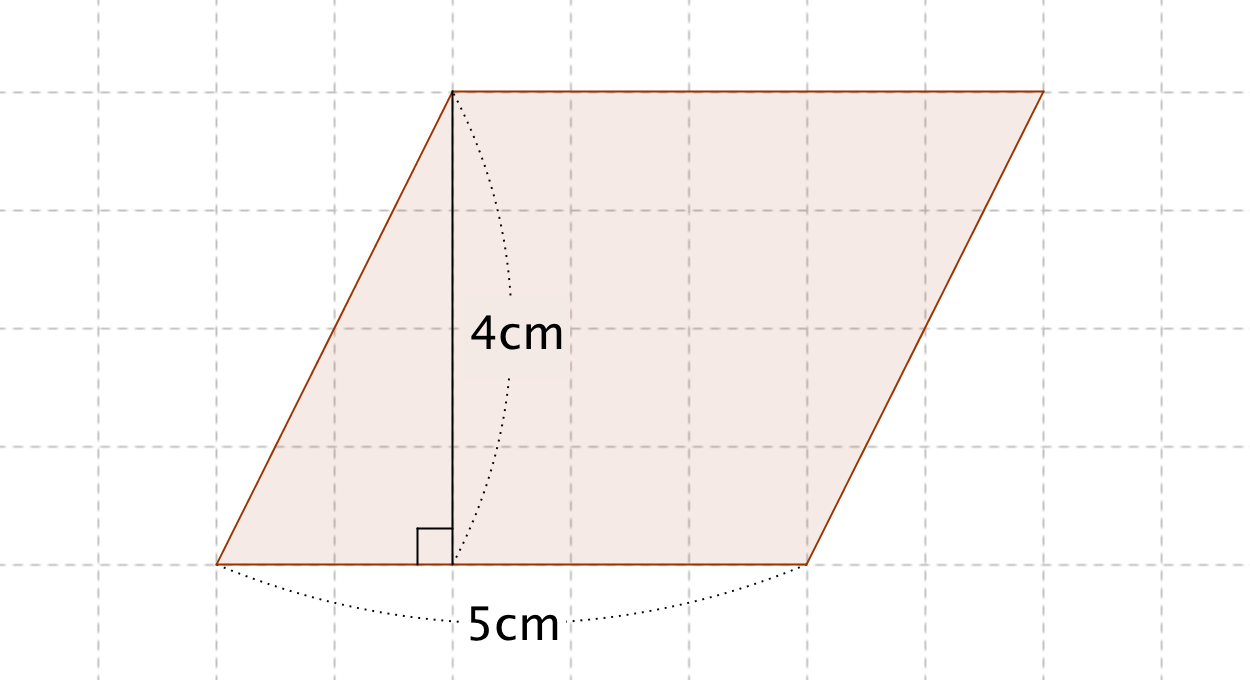
平行四辺形の面積の公式 算数の公式

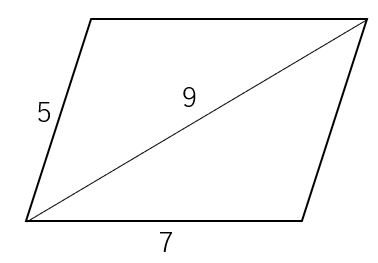
面積 平行四辺形の面積の変わった求め方の問題 数学の要点まとめ 練習問題一覧

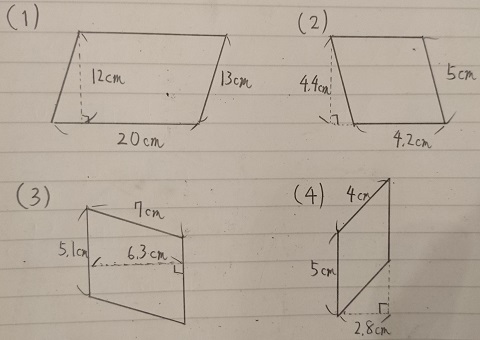
平行四辺形の面積 算数 一般常識クイズ一問一答問題まとめ

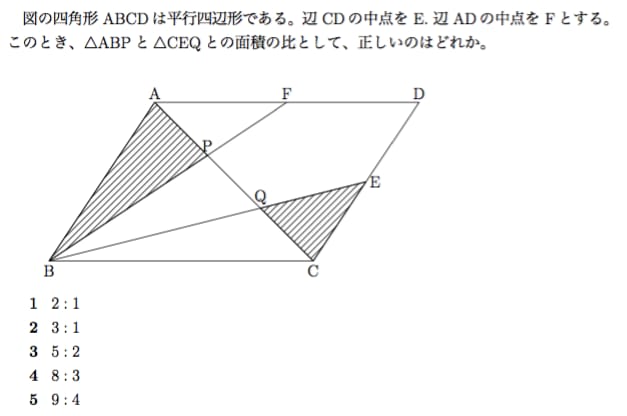
平行四辺形 中点 2つの三角形の面積比 知能問題 数的処理 判断推理 数的推理 数学パズル ｓｐｉ 空間把握 解いてみてください

算数パズル 10秒で解けますか 公式を使わない平行四辺形の面積問題 Youtube

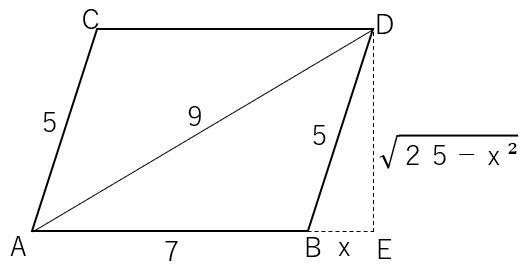
面積 平行四辺形の面積の変わった求め方の問題 数学の要点まとめ 練習問題一覧

Dfeの面積と平行四辺形の面積比の問題です Clearnote

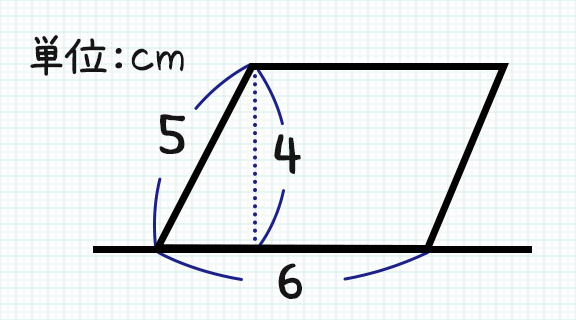
毎日脳トレ この平行四辺形の面積わかる Dアプリ レビュー

平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は４つ 中学や高校の数学の計算問題

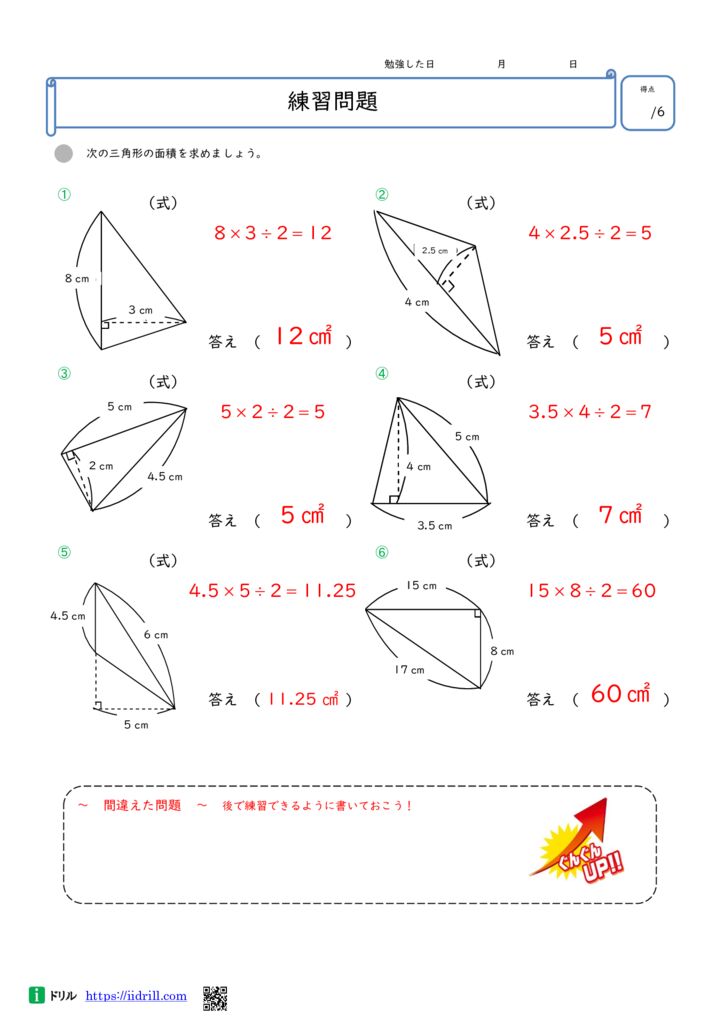
5年生算数ドリル 面積

図形問題が驚くほど得意になる基本問題とは あおぞら塾

中学受験算数 平行四辺形の面積を求める問題 Okwave

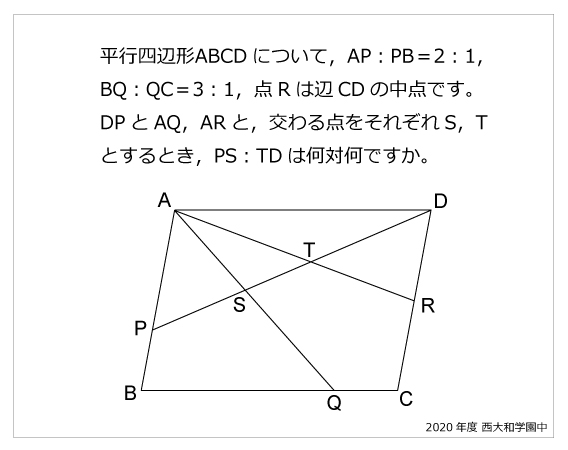
平行四辺形 算数星人のweb問題集 中学受験算数の問題に挑戦

3

この平行四辺形 面積の比は パズル算数クイズ

1

正方形と平行四辺形の面積の話 クイズ あなたは小学５年生より賢いの 12 25 何ゴト

面白い数学の問題 平行四辺形の中の三角形 平行四辺形って覚えてますか そらの暇つぶしch

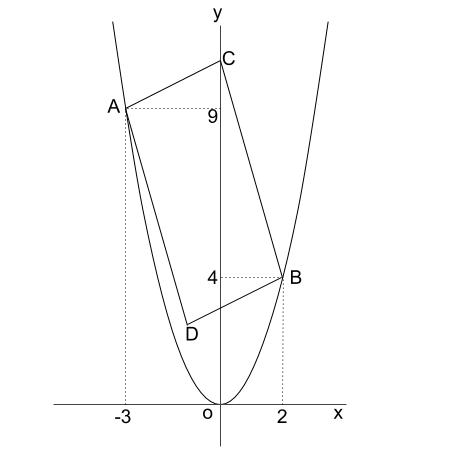
2乗に比例 平行四辺形の面積 中学数学の無料オンライン学習サイトchu Su

数学の問題で分からないので教えてください 図のような平行四辺形abcdで Yahoo 知恵袋

今月の問題 平行四辺形の中の三角形の問題

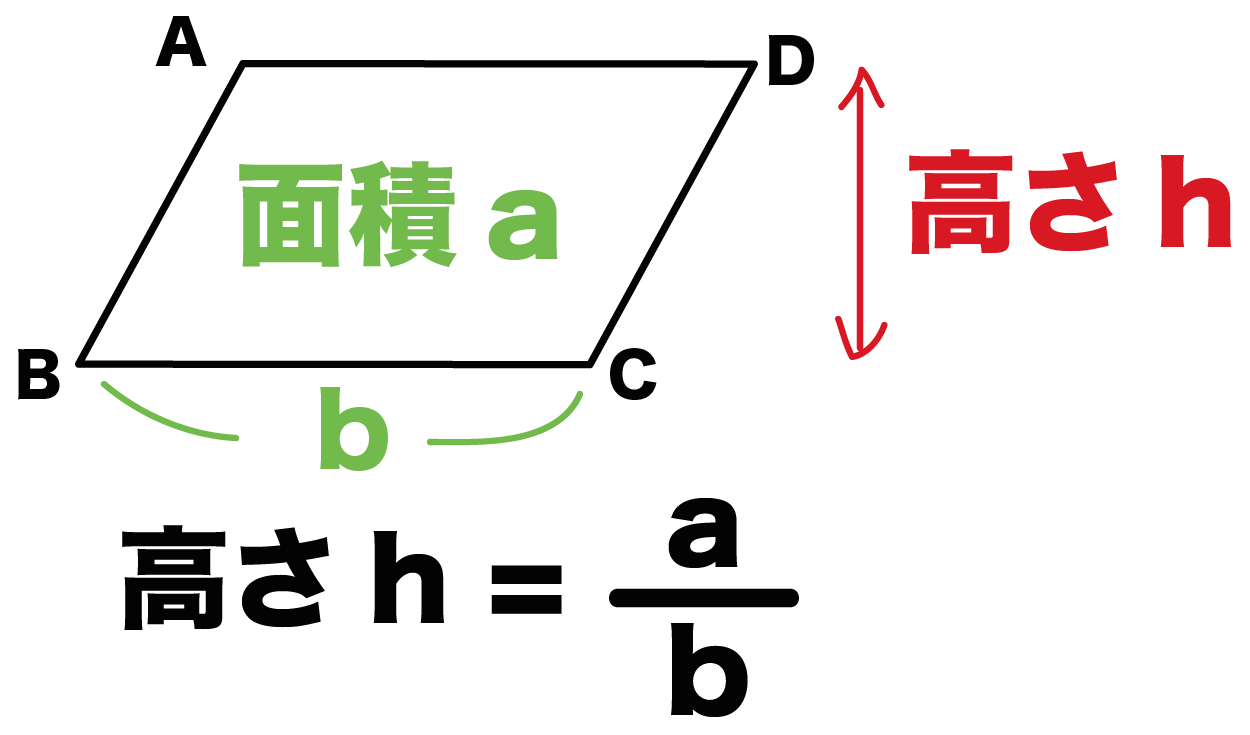
中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく

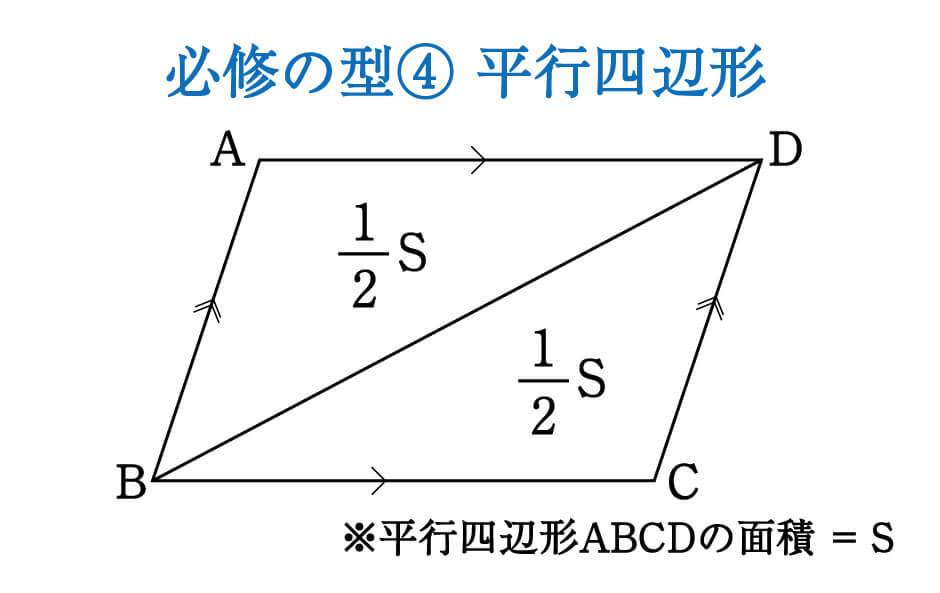
数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

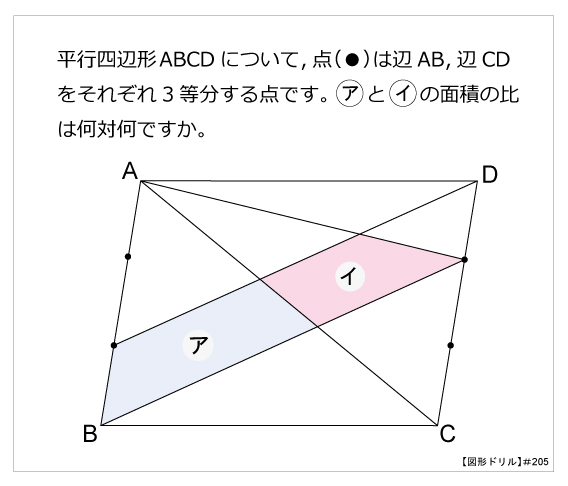
第5問 平行四辺形内の面積比 図形ドリル 第5問 平行四辺形内の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦

平行四辺形の面積を求める公式 あまり知られていないかも 中学や高校の数学の計算問題

平行四辺形を分ける面積比の求め方 算数解法の極意

小５ 算数 小５ ４１ 平行四辺形の面積 Youtube

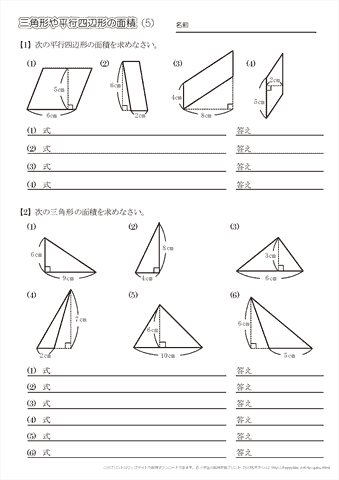
小学５年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生

等積変形を用いる面積問題 14年 早稲田中学校 恋する中高一貫校 適性検査 徹底攻略

平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun